Stelling van Pythagoras deel 3 bereken de schuine zijde wiskunde tv YouTube
Berekenen

De stelling van Pythagoras voor deze driehoek is AB 2 + AC 2 = BC 2. Als je de lengte van zijde AB en zijde BC weet, kun je de lengte van zijde AC berekenen. 4 2 + AC 2 = 5 2. 16 + AC 2 = 25. AC 2 = 25 - 16 = 9 $$AC = \sqrt{9} = 3$$ De stelling van Pythagoras kun je alleen gebruiken bij een rechthoekige driehoek. Als je van een driehoek de.
PPT De stelling van Pythagoras PowerPoint Presentation, free download ID3915661

Bij de stelling van Pythagoras kan je de schuine zijde berekenen wanneer je de 2 rechthoekszijden weet. De stelling wordt vaak aangegeven als a 2 + b 2 = c 2. Hierin zijn a en b de rechthoekszijden en c de schuine zijde. De langste zijde berekenen met de stelling van Pythagoras.
PPT De Stelling van Pythagoras PowerPoint Presentation, free download ID3535647

De stelling van Pythagoras is een van de bekendste wiskunde formules. De stelling luidt: de som van het kwadraat van de lengtes van de rechthoekszijden is gelijk aan het kwadraat van de lengte van de schuine zijde. Kortom: A 2 + B 2 = C 2 Hierbij is A de lengte van de korte zijde, B de lengte van de lange zijde en C de lengte van de schuine zijde.
Uitleg Verlengde Stelling van Pythagoras YouTube

De stelling van Pythagoras stelt dat de som van de kwadraten van de lengten van de twee benen van een rechthoekige driehoek gelijk is aan het kwadraat van de lengte van de schuine zijde. Dit kan wiskundig worden uitgedrukt als: a² + b² = c². Waarbij a en b de lengtes van de twee benen van de driehoek zijn, en c de lengte van de schuine zijde.
Pythagoras basis voorbeeld oefeningen oplossen met de stelling YouTube

Maak eerst een keuze welke driehoek je gaat gebruiken. Geef de hoekpunten en lengten van 2 zijden op. Klik daarna op "Berekenen". Je krijgt dan de uitwerking met de Stelling van Pythagoras. Handig als naslagwerk bij opgaven uit je boek! Laat steeds 1 van de 3 zijden leeg!
Stelling van Pythagoras en bekende driehoeken YouTube

De stelling van Pythagoras is een wiskundige stelling die het verband geeft tussen de lengten van de zijden van een rechthoekige driehoek: In een rechthoekige driehoek is de som van de kwadraten van de lengtes van de rechthoekszijden gelijk aan het kwadraat van de lengte van de schuine zijde.
Slimleren Introductie van de Stelling van Pythagoras
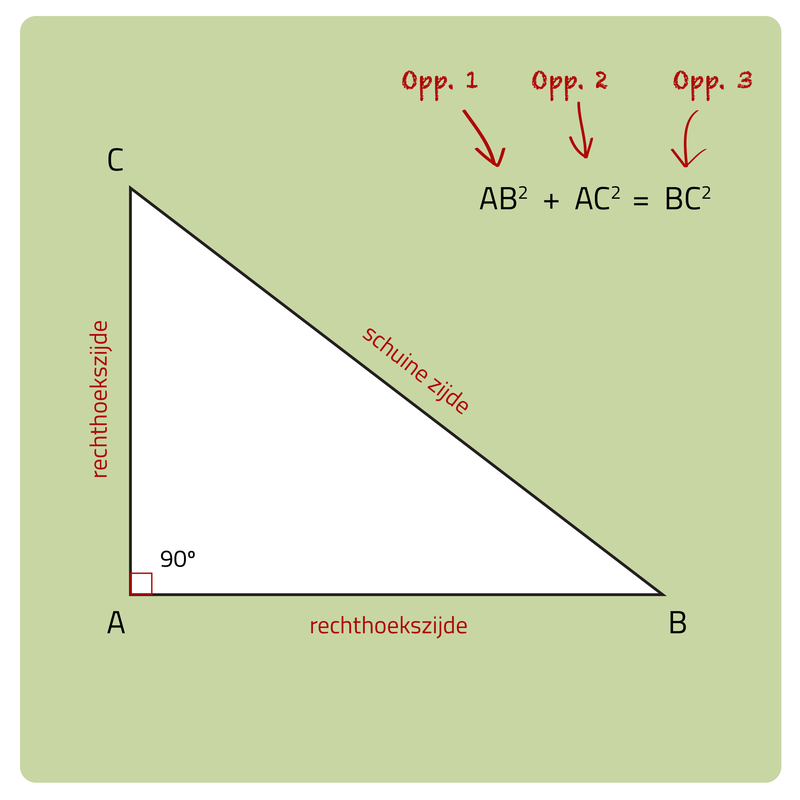
De stelling van Pythagoras beschrijft een speciaal verband tussen de zijden van een rechthoekige driehoek. Heel vroeger was de mensheid al bekend met dit verband. In dit onderwerp gaan we uitzoeken hoe je de stelling van Pythagoras kan gebruiken en bewijzen we waarom het werkt. Stelling van Pythagoras. Leren. Inleiding in de stelling van Pythagoras
De stelling van Pythagoras StudyGo

De stelling van Pythagoras kun je alleen gebruiken bij een driehoek waar één hoek in zit van 90 graden. Dit betekent dat de hoek loodrecht is. Met deze formule kun je de zijdes van een driehoek berekenen. De stelling van Pythagoras is a 2 + b 2 = c 2.
Stelling van Pythagoras deel 4 bereken de rechthoekszijde wiskunde tv YouTube

Videotranscript. In deze video zullen we uitleg geven over de stelling van Pythagoras, wat een zeer leuk onderwerp is. Als je meer en meer wiskunde leert zal je zien dat het een van de pilaren is waarop de wiskunde verderbouwt. Het is nuttig in de meetkunde, het is eigenlijk de ruggengraat van de meetkunde.
Slimleren Stelling van Pythagoras schuine zijde berekenen en toepassen in een
Beschrijving Begrippen. In deze uitlegvideo voor wiskunde gaan we laten zien hoe we hoeken berekenen met de tangens, sinus en cosinus. Ook gaan we zijden berekenen met de Stelling van Pythagoras. Hierbij kijken we naar het verschil tussen de schuine, overstaande en aanliggende zijde en zullen we de hellingshoek bespreken.
Stelling van Pythagoras Hoe werkt het? DEES Amsterdam
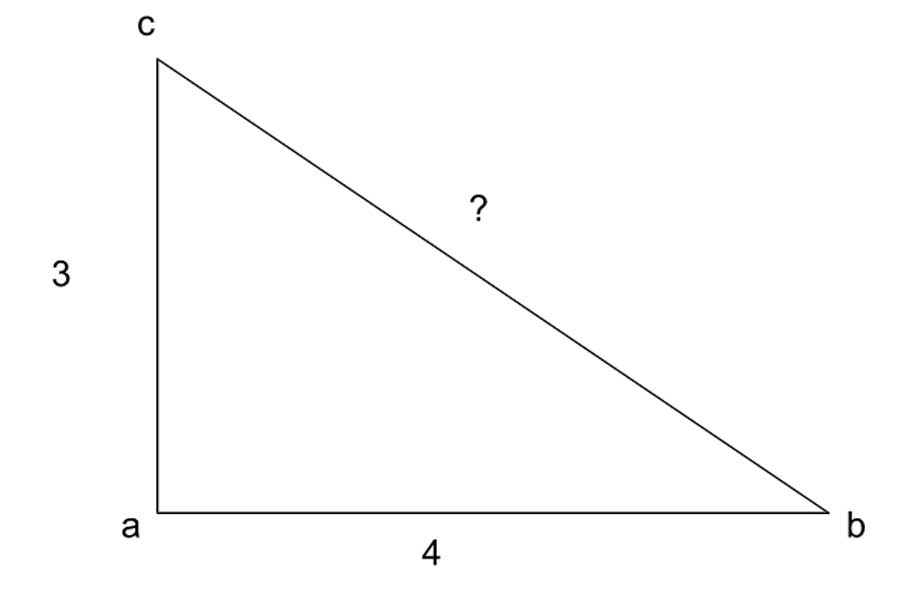
Stelling van Pythagoras. Deze wiskundige stelling is vernoemd naar de Griekse wiskundige Pythagoras. In zijn stelling geeft hij aan dat bij een rechthoekige driehoek, de de som van de kwadranten van de lengtes van de rechthoekszijden gelijk is aan het kwadraat van de lengte van de schuine zijde. Voorbeeld.
Stelling Van Pythagoras Ontdek De Piramide Geheimen

Met behulp van de stelling van Pythagoras vind je de cosinusregel: a2 = b2 + c2 − 2bccos(α). Daar zijn drie varianten van. Met deze twee regels kun je vanuit drie gegevens alle zijden en hoeken van een willekeurige driehoek berekenen. Dat heet "triangulatie" (driehoeksmeting).
Oefening stelling van Pythagoras GeoGebra
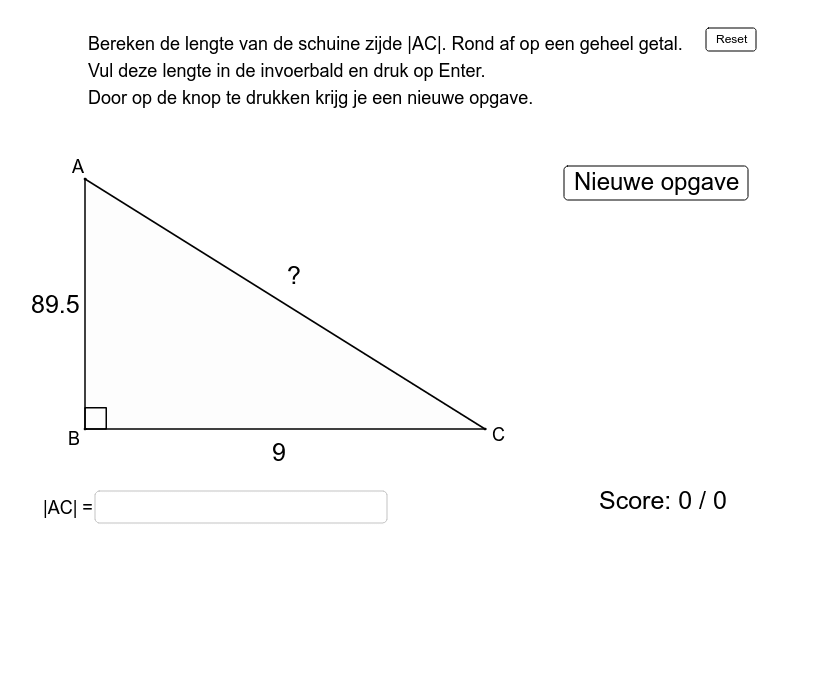
Subscribed. 1.8K. 227K views 10 years ago Pythagoras. Ga naar http://www.WiskundeAcademie.nl/onderw. voor nog meer gratis uitlegvideo's over toepassingen van de stelling van Pythagoras.
De stelling van Pythagoras 5. Een zijde berekenen met Pythagoras YouTube

De stelling van Pythagoras beschrijft een speciaal verband tussen de zijden van een rechthoekige driehoek. Heel vroeger was de mensheid al bekend met dit verband. In dit onderwerp gaan we uitzoeken hoe je de stelling van Pythagoras kan gebruiken en bewijzen we waarom het werkt. Stelling van Pythagoras. Leren. Inleiding in de stelling van Pythagoras
Wiskunde De stelling van Pythagoras YouTube

In de rechthoekige driehoek geldt de stelling van pythagoras: a² + b² = c². Dit betekent dat c gelijk is aan de vierkantswortel van (a² + b²) of b gelijk is aan de vierkantswortel van (c² - a²). Verder gelden voor de delen van de hypotenusa (p en q genoemd, p onder a en q onder b) deze formules:
Stelling van Pythagoras II YouTube

De stelling van pythagoras kan als volgt worden geschreven: a² + b² = c², Waarbij a en b de lengtes zijn van de kortere zijden, of benen, van een rechthoekige driehoek, en c - de lengte is van de langste zijde of schuine zijde.